Your Voronoi delaunay duality images are ready. Voronoi delaunay duality are a topic that is being searched for and liked by netizens today. You can Download the Voronoi delaunay duality files here. Download all royalty-free photos.
If you’re looking for voronoi delaunay duality images information linked to the voronoi delaunay duality topic, you have pay a visit to the right blog. Our website frequently provides you with suggestions for viewing the highest quality video and picture content, please kindly search and find more enlightening video articles and images that match your interests.
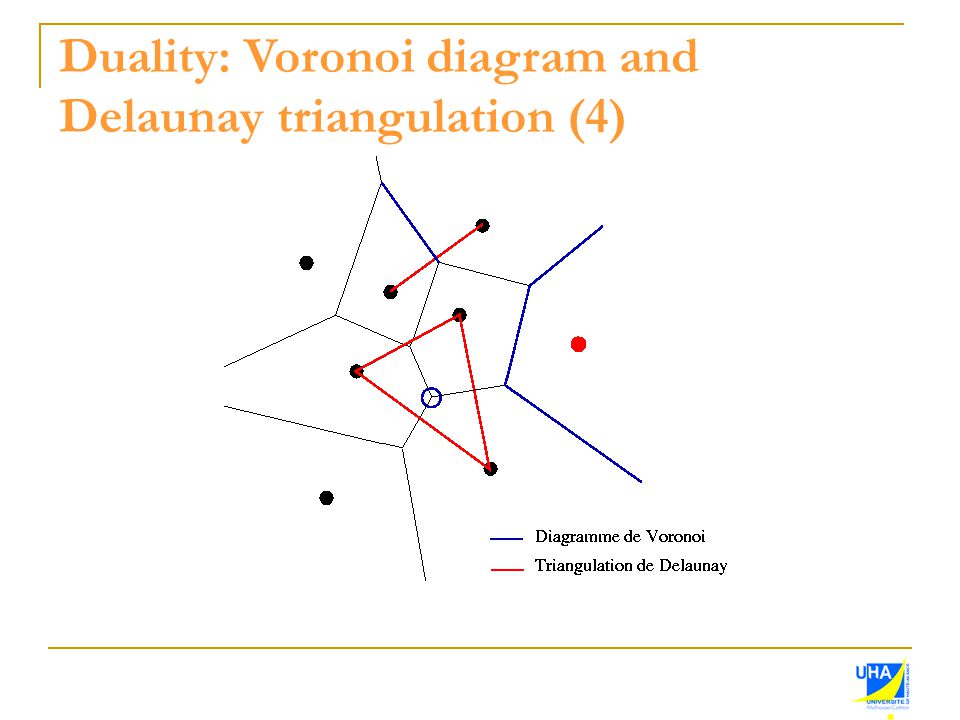
Voronoi Delaunay Duality. Voronoi-Delaunay duality and Delaunay meshes January 2007 DOI. 101145 12362461236306 Source DBLP Conference. Triangulations can be used to establish a Voronoi-Delaunay duality on pwf surfaces which to the best of our knowl-edge has not been done before. 23 Delaunay - Voronoi Duality 6 Figure 4.
Voronoi Diagram Delaunay Triangulation And Their Duality Download Scientific Diagram From researchgate.net
We introduce the constrained Voronoi diagram of a planar straight-line graph containing n vertices or sites where the line segments of the graph are regarded as obstacles and show that an extended version of this diagram is the dual of the constrained Delaunay triangulation. We utilize the fact that the user location cannot be recovered if only given an irregular. The Euclidean Delaunay triangulation DTEP is the geometric dual of the Voronoi diagram. We first propose the notion of well-formed Voronoi diagrams and establish a precise dual relationship between them and proper Delaunay triangulations on pwf surfaces. We define a Delaunay mesh to be a manifold triangle mesh whose edges form an intrinsic Delaunay triangulation or iDT of its vertices where the triangulated domain is the piecewise flat mesh surface. In this work we propose a novel framework based on the classical geometric structure the so-called Voronoi-Delaunay Duality VDD.
The Euclidean Delaunay triangulation DTEP is the geometric dual of the Voronoi diagram.
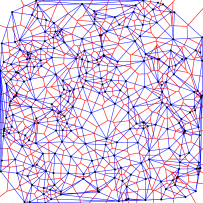
Proceedings of the 2007 ACM Symposium on Solid and Physical Modeling Beijing China. Heres a larger example showing the relationship with Voronoi polygon centers in red and corners in blue and the Voronoi edges in white and the Delaunay triangulation in black. D-min vertex of at least one dd 2e-face of P vertices of P 2 dd 2e-faces of P. We introduce the constrained Voronoi diagram of a planar straight-line graph containing n vertices or sites where the line segments of the graph are regarded as obstacles and show that an extended version of this diagram is the dual of the constrained Delaunay triangulation. C same as b. Incremental Delaunay triangulations and Voronoi diagrams by Frank Bossen Voronoi DiagramDelaunay Triangulation by Paul Chew uses a randomized incremental algorithm with brute force point location.
Source: researchgate.net
2-Site Voronoi diagrams by Matt Dickerson from the Middlebury College Undergraduate Research Project in Computational Geometry. We establish a precise dual relationship between the iDT and the Voronoi tessellation of the vertices of a piecewise flat pwf surface and exploit this duality to demonstrate criteria which ensure the existence of a proper Delaunay triangulation. We briefly discuss O n log n algorithms for constructing the extended. Möller Torsten 2007-06-04 000000 Voronoi-Delaunay Duality and Delaunay Meshes Ramsay Dyer GrUVi Lab School of Computing We show that meshes constructed from a smooth surface by taking an iDT or a restricted Delaunay triangulation do not in general yield a Delaunay mesh. Thus corners in the Delaunay triangulation are polygons in the Voronoi diagram and vice versa.
Source: deepai.org
In computational geometry the duality between Voronoi diagrams and Delaunay triangulations implies that any algorithm for constructing a Voronoi diagram can be immediately converted into an algorithm for the Delaunay. In this work we propose a novel geometric framework based on the classical discrete geometric structure the Voronoi-Delaunay duality VDD. 2-Site Voronoi diagrams by Matt Dickerson from the Middlebury College Undergraduate Research Project in Computational Geometry. We utilize the fact that the user location cannot be recovered if only given an irregular. The Euclidean Delaunay triangulation DTEP is the geometric dual of the Voronoi diagram.
Source: slideplayer.com
We first propose the notion of well-formed Voronoi diagrams and establish a precise dual relationship between them and proper Delaunay triangulations on pwf surfaces. Dd 2eedges incident to a vertex p are in h. Then we provide an algorithm which given any input manifold. 23 Delaunay - Voronoi Duality 6 Figure 4. The Euclidean Delaunay triangulation DTEP is the geometric dual of the Voronoi diagram.
Source: quora.com
This duality means that I can represent the two graphs together. We establish a precise dual relationship between the iDT and the Voronoi tessellation of the vertices of a piecewise flat pwf surface and exploit this duality to demonstrate criteria which ensure the existence of a proper Delaunay triangulation. In this work we propose a novel geometric framework based on the classical discrete geometric structure the Voronoi-Delaunay duality VDD. Proceedings of the 2007 ACM Symposium on Solid and Physical Modeling Beijing China. P is a x.
Source: researchgate.net
P is a x. Dd 2eedges incident to a vertex p are in h. A A 1-Simplex mesh and its dual. Delaunay Voronoi Duality. We define a Delaunay mesh to be a manifold triangle mesh whose edges form an intrinsic Delaunay triangulation or iDT of its vertices where the triangulated domain is the piecewise flat mesh surface.
Source: github.com
Table I gives the symbols used in the work. Delaunay Voronoi Duality. Voronoi-Delaunay duality and Delaunay meshes January 2007 DOI. 101145 12362461236306 Source DBLP Conference. D-min vertex of at least one dd 2e-face of P vertices of P 2 dd 2e-faces of P.
Source: scicomp.stackexchange.com
Proceedings of the 2007 ACM Symposium on Solid and Physical Modeling Beijing China. In this work we propose a novel framework based on the classical geometric structure the so-called Voronoi-Delaunay Duality VDD. We first propose the notion of well-formed Voronoi diagrams and establish a precise dual relationship between them and proper Delaunay triangulations on pwf surfaces. Voronoi-Delaunay duality and Delaunay meshes Dyer Ramsay. We briefly discuss O n log n algorithms for constructing the extended.
Source: researchgate.net
We utilize the fact that the user location cannot be recovered if only given an irregular. We establish a precise dual relationship between the iDT and the Voronoi tessellation of the vertices of a piecewise flat pwf surface and exploit this duality to demonstrate criteria which ensure the existence of a proper Delaunay triangulation. C same as b. The dual of the triangulation boundary is considered to extract the simplex mesh. 2-Site Voronoi diagrams by Matt Dickerson from the Middlebury College Undergraduate Research Project in Computational Geometry.
Source: stackoverflow.com
We establish a precise dual relationship between the iDT and the Voronoi tessellation of the vertices of a piecewise flat pwf surface and exploit this duality to demonstrate criteria which ensure the existence of a proper Delaunay triangulation. A A 1-Simplex mesh and its dual. Möller Torsten 2007-06-04 000000 Voronoi-Delaunay Duality and Delaunay Meshes Ramsay Dyer GrUVi Lab School of Computing We show that meshes constructed from a smooth surface by taking an iDT or a restricted Delaunay triangulation do not in general yield a Delaunay mesh. For example in the case when the voronoi tessellation is a regular square grid. We define a Delaunay mesh to be a manifold triangle mesh whose edges form an intrinsic Delaunay triangulation or iDT of its vertices where the triangulated domain is the piecewise flat mesh surface.
Source: researchgate.net
Dd 2eedges incident to a vertex p are in h. A A 1-Simplex mesh and its dual. We show that meshes constructed from a smooth surface by taking an iDT or a restricted Delaunay triangulation do not in general yield a Delaunay mesh. Then we provide an algorithm which given any input manifold. 101145 12362461236306 Source DBLP Conference.
Source: geom.uiuc.edu
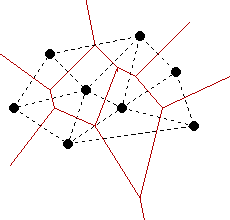
We define a Delaunay mesh to be a manifold triangle mesh whose edges form an intrinsic Delaunay triangulation or iDT of its vertices where the triangulated domain is the piecewise flat mesh surface. 1 we treat the user location O as the center and properly select n discrete points C C 0 C 1. 23 Delaunay - Voronoi Duality 6 Figure 4. Delaunay later dened the Delaunay triangulation and found it to be the same as the dual of the Voronoi Diagram. This duality means that I can represent the two graphs together.
Source: researchgate.net
D-min vertex of at least one dd 2e-face of P vertices of P 2 dd 2e-faces of P. Delaunay later dened the Delaunay triangulation and found it to be the same as the dual of the Voronoi Diagram. Voronoi himself was the rst to consider the dual of the Voronoi Diagram where any two points whose Voronoi regions have boundary in common are connected by an edge. 2A k-face is the intersection of d k hyperplanes defining P. Delaunay Voronoi Duality.
Source: github.com
In general the dual of the Voronoi diagram will not be a proper triangulation. In general the dual of the Voronoi diagram will not be a proper triangulation. We utilize the fact that the user location cannot be recovered if only given an irregular. In this work we propose a novel framework based on the classical geometric structure the so-called Voronoi-Delaunay Duality VDD. We introduce the constrained Voronoi diagram of a planar straight-line graph containing n vertices or sites where the line segments of the graph are regarded as obstacles and show that an extended version of this diagram is the dual of the constrained Delaunay triangulation.
Source: researchgate.net
In general the dual of the Voronoi diagram will not be a proper triangulation. The dual of the triangulation boundary is considered to extract the simplex mesh. The simple answer is that they are dual because for every delaunay triangulation there exists one and only one corresponding voronoi tessellation and vise versa. Delaunay later dened the Delaunay triangulation and found it to be the same as the dual of the Voronoi Diagram. Dd 2eedges incident to a vertex p are in h.
Source: researchgate.net
In computational geometry the duality between Voronoi diagrams and Delaunay triangulations implies that any algorithm for constructing a Voronoi diagram can be immediately converted into an algorithm for the Delaunay. Voronoi-Delaunay duality and Delaunay meshes Dyer Ramsay. We utilize the fact that the user location cannot be recovered if only given an irregular. For further reading on these extensively studied data structures see for instance 231020. K-faces n d k Ond k dd 2e-faces Onb.
Source: researchgate.net
Voronoi himself was the rst to consider the dual of the Voronoi Diagram where any two points whose Voronoi regions have boundary in common are connected by an edge. Each cell VEpi of the Voronoi diagram can i. 2-Site Voronoi diagrams by Matt Dickerson from the Middlebury College Undergraduate Research Project in Computational Geometry. 101145 12362461236306 Source DBLP Conference. K-faces n d k Ond k dd 2e-faces Onb.
Source: researchgate.net
In general the dual of the Voronoi diagram will not be a proper triangulation. Möller Torsten 2007-06-04 000000 Voronoi-Delaunay Duality and Delaunay Meshes Ramsay Dyer GrUVi Lab School of Computing We show that meshes constructed from a smooth surface by taking an iDT or a restricted Delaunay triangulation do not in general yield a Delaunay mesh. Heres a larger example showing the relationship with Voronoi polygon centers in red and corners in blue and the Voronoi edges in white and the Delaunay triangulation in black. As shown in Fig. Delaunay Voronoi Duality.
Source: slideplayer.com
Triangulations can be used to establish a Voronoi-Delaunay duality on pwf surfaces which to the best of our knowl-edge has not been done before. We define a Delaunay mesh to be a manifold triangle mesh whose edges form an intrinsic Delaunay triangulation or iDT of its vertices where the triangulated domain is the piecewise flat mesh surface. Xd xdp or in h. Heres a larger example showing the relationship with Voronoi polygon centers in red and corners in blue and the Voronoi edges in white and the Delaunay triangulation in black. Triangulations can be used to establish a Voronoi-Delaunay duality on pwf surfaces which to the best of our knowl-edge has not been done before.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site value, please support us by sharing this posts to your favorite social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title voronoi delaunay duality by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
