Your Voronoi diagram algorithm complexity images are ready. Voronoi diagram algorithm complexity are a topic that is being searched for and liked by netizens now. You can Get the Voronoi diagram algorithm complexity files here. Download all free vectors.
If you’re searching for voronoi diagram algorithm complexity images information connected with to the voronoi diagram algorithm complexity topic, you have pay a visit to the right site. Our website always provides you with suggestions for downloading the maximum quality video and picture content, please kindly search and locate more informative video articles and images that fit your interests.
Voronoi Diagram Algorithm Complexity. The Voronoi diagram computation is cast into a clustering problem in the discrete voxelpixel space. Fortunes algorithm is a sweep line algorithm for generating a Voronoi diagram from a set of points in a plane using O n log n time and O n space. The Voronoi Diagram of Xin RN is defined as n Voronoi cells C fW ign 1 where Wi fx 2R N jkx xik kx xjk8j 6ig. It was originally published by Steven Fortune in 1986 in his paper A sweepline algorithm for Voronoi diagrams.
Voronoi Diagram Of A Set Of Points On The Left And Its Dual Delaunay Download Scientific Diagram From researchgate.net
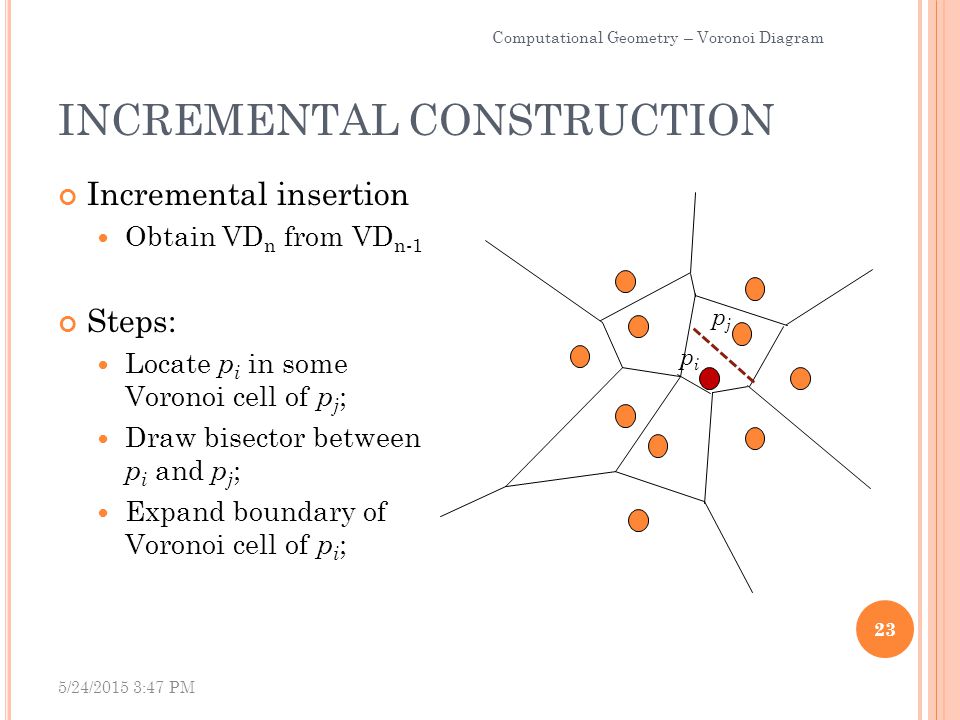
Each region in the variable gadget will contain at least one Voronoi region. Fortunes algorithm improves the diagram creation by using two lines moving through the map iteratively building the Voronoi sites. We introduce a geometric transformation that allows Voronoi diagrams to be computed using a sweepline technique. We study algorithms and combinatorial complexity bounds for emph stable-matching Voronoi diagrams where a set S of n point sites in. In particular the Voronoi diagram of a set of points with rational coordinates itself has rational coordinates so you can do everything with integer arithmetic and. For n 3 v 2n 5 and e 3n 6 Proof.
The Voronoi diagram is just a diagram.
However as is often the case constructions that realize the quadratic complexity of say the weighted multiplicative Voronoi diagram in the plane are somewhat contrived. General Case For Voronoi graphs f n v 1 e n 2 p e i p To apply Eulers Formula we planarize the Voronoi. Fortunes algorithm improves the diagram creation by using two lines moving through the map iteratively building the Voronoi sites. I think the paper Approximating the Medial Axis from the Voronoi Diagram with a Convergence Guarantee might be helpful. The naive implementation for calculating Voronoi Diagrams is O n2 complex. In particular the Voronoi diagram of a set of points with rational coordinates itself has rational coordinates so you can do everything with integer arithmetic and.
Source: slideplayer.com
By definition a Voronoi diagram contains exactly one point in each region. The Voronoi Diagram of Xin RN is defined as n Voronoi cells C fW ign 1 where Wi fx 2R N jkx xik kx xjk8j 6ig. We introduce a geometric transformation that allows Voronoi diagrams to be computed using a sweepline technique. Previous work on the stable-matching Voronoi diagram provided existence and uniqueness proofs but did not analyze its combinatorial or algorithmic complexity. Each region in the variable gadget will contain at least one Voronoi region.
Source: slidetodoc.com
To each point p2S the Voronoi diagram of Sassociates a region VRp such that VRp fx2Ejdxp dxq8q2Sg 1 It is a subdivision of the space where each point from Sis associated with a region of the space closest to it. In this paper we show that a stable-matching Voronoi diagram of. The Voronoi diagram computation is cast into a clustering problem in the discrete voxelpixel space. Fortunes algorithm improves the diagram creation by using two lines moving through the map iteratively building the Voronoi sites. We introduce a geometric transformation that allows Voronoi diagrams to be computed using a sweepline technique.
Source: math.stackexchange.com
By definition a Voronoi diagram contains exactly one point in each region. Constructing Voronoi Diagrams Half plane intersection O n2 log n Fortunes Algorithm Sweep line algorithm Voronoi diagram constructed as horizontal line sweeps the set of sites from top to bottom diagram which cannot. The Voronoi diagram is just a diagram. Constructing the diagram would not change the asymptotic complexity of your problem although it would make your problem more complicated and less memory efficient. The naive implementation for calculating Voronoi Diagrams is O n2 complex.
Source: slideshare.net
You just have to be in a computational setting where you can do arithmetic on your original coordinates. The transformation is used to obtain simple algorithms for computing the Voronoi diagram of point sites of line segment sites and of weighted point sites. By definition a Voronoi diagram contains exactly one point in each region. Constructing Voronoi Diagrams Half plane intersection O n2 log n Fortunes Algorithm Sweep line algorithm Voronoi diagram constructed as horizontal line sweeps the set of sites from top to bottom diagram which cannot. However as is often the case constructions that realize the quadratic complexity of say the weighted multiplicative Voronoi diagram in the plane are somewhat contrived.
Source: researchgate.net
Previous work on the stable-matching Voronoi diagram provided existence and uniqueness proofs but did not analyze its combinatorial or algorithmic complexity. The Voronoi diagram is a well-known geometric structure with a broad spectrum of applications in computational geometry and other areas of Computer Science eg see Aurenhammer1991 bookAurenhammer Brandt1992 Kise1998 Meguerdichian2001 Petrek2007 Stojmenovic2006 Bhattacharya2008. Fortunes algorithm improves the diagram creation by using two lines moving through the map iteratively building the Voronoi sites. The Voronoi diagram partitions the plane into regions. The Voronoi diagram is just a diagram.
Source: researchgate.net
You just have to be in a computational setting where you can do arithmetic on your original coordinates. Constructing Voronoi Diagrams Half plane intersection O n2 log n Fortunes Algorithm Sweep line algorithm Voronoi diagram constructed as horizontal line sweeps the set of sites from top to bottom diagram which cannot. The Voronoi diagram computation is cast into a clustering problem in the discrete voxelpixel space. The naive implementation for calculating Voronoi Diagrams is O n2 complex. I think the paper Approximating the Medial Axis from the Voronoi Diagram with a Convergence Guarantee might be helpful.
Source: gist.github.com
It was originally published by Steven Fortune in 1986 in his paper A sweepline algorithm for Voronoi diagrams. Their complexity becomes quadratic in the worst case. So the computational complexity of Voronoi-diagram computation is well-defined. The naive implementation for calculating Voronoi Diagrams is O n2 complex. Constructing Voronoi Diagrams Half plane intersection O n2 log n Fortunes Algorithm Sweep line algorithm Voronoi diagram constructed as horizontal line sweeps the set of sites from top to bottom diagram which cannot.
Source: slidetodoc.com
By definition a Voronoi diagram contains exactly one point in each region. The Voronoi diagram is a well-known geometric structure with a broad spectrum of applications in computational geometry and other areas of Computer Science eg see Aurenhammer1991 bookAurenhammer Brandt1992 Kise1998 Meguerdichian2001 Petrek2007 Stojmenovic2006 Bhattacharya2008. We study algorithms and combinatorial complexity bounds for emph stable-matching Voronoi diagrams where a set S of n point sites in. This immediately tells us that a minimal Voronoi cover for a variable gadget will have at least eighteen points. A simple algorithm that I have seen to work with some polygonal shapes works like this.
Source: researchgate.net
By definition a Voronoi diagram contains exactly one point in each region. However as is often the case constructions that realize the quadratic complexity of say the weighted multiplicative Voronoi diagram in the plane are somewhat contrived. Previous work on the stable-matching Voronoi diagram provided existence and uniqueness proofs but did not analyze its combinatorial or algorithmic complexity. So the computational complexity of Voronoi-diagram computation is well-defined. Each region in the variable gadget will contain at least one Voronoi region.
Source: researchgate.net
The Voronoi diagram partitions the plane into regions. The Voronoi diagram partitions the plane into regions. The naive implementation for calculating Voronoi Diagrams is O n2 complex. To each point p2S the Voronoi diagram of Sassociates a region VRp such that VRp fx2Ejdxp dxq8q2Sg 1 It is a subdivision of the space where each point from Sis associated with a region of the space closest to it. Fortunes algorithm is a sweep line algorithm for generating a Voronoi diagram from a set of points in a plane using O n log n time and O n space.
Source: researchgate.net
The Voronoi diagram is a well-known geometric structure with a broad spectrum of applications in computational geometry and other areas of Computer Science eg see Aurenhammer1991 bookAurenhammer Brandt1992 Kise1998 Meguerdichian2001 Petrek2007 Stojmenovic2006 Bhattacharya2008. Each region in the variable gadget will contain at least one Voronoi region. I dont think its suited to finding the nearest point in a set. In this paper we show that a stable-matching Voronoi diagram of. On bigger diagrams with hundreds or thousands of sites a better algorithm is preferred.
Source: present5.com
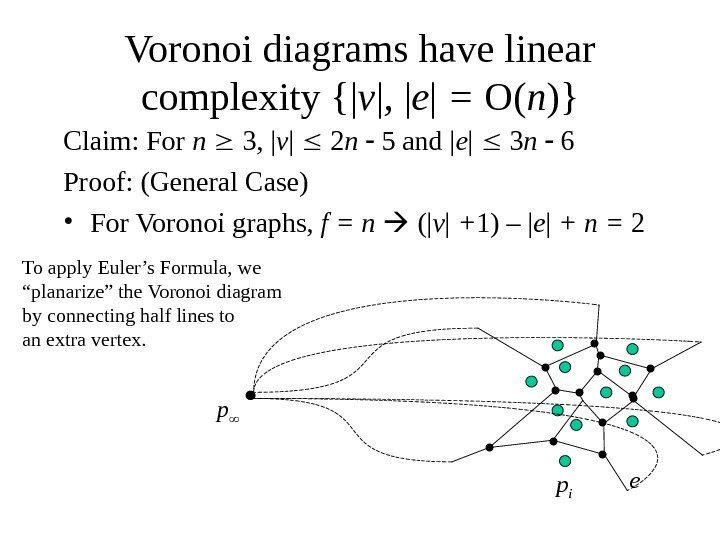
Proof of Space Complexity We look at Dual of Voronoi Diagram Delaunay Triangulation Voronoi vertices are Delaunay faces f Voronoi edges are Delaunay edges e We need to bound both f and e. Proof of Space Complexity We look at Dual of Voronoi Diagram Delaunay Triangulation Voronoi vertices are Delaunay faces f Voronoi edges are Delaunay edges e We need to bound both f and e. Constructing Voronoi Diagrams Half plane intersection O n2 log n Fortunes Algorithm Sweep line algorithm Voronoi diagram constructed as horizontal line sweeps the set of sites from top to bottom diagram which cannot. The Voronoi diagram partitions the plane into regions. However as is often the case constructions that realize the quadratic complexity of say the weighted multiplicative Voronoi diagram in the plane are somewhat contrived.
Source: researchgate.net
So the computational complexity of Voronoi-diagram computation is well-defined. However as is often the case constructions that realize the quadratic complexity of say the weighted multiplicative Voronoi diagram in the plane are somewhat contrived. I think the paper Approximating the Medial Axis from the Voronoi Diagram with a Convergence Guarantee might be helpful. Each region in the variable gadget will contain at least one Voronoi region. Not a data structure or algorithm.
Source: slideshare.net
It was originally published by Steven Fortune in 1986 in his paper A sweepline algorithm for Voronoi diagrams. Present an n-body proximity query algorithm based on computing the discrete 2ndorder Voronoi diagram on the GPU. The Voronoi diagram computation is cast into a clustering problem in the discrete voxelpixel space. Not a data structure or algorithm. The Voronoi diagram is a well-known geometric structure with a broad spectrum of applications in computational geometry and other areas of Computer Science eg see Aurenhammer1991 bookAurenhammer Brandt1992 Kise1998 Meguerdichian2001 Petrek2007 Stojmenovic2006 Bhattacharya2008.
Source: slideshare.net
Each region in the variable gadget will contain at least one Voronoi region. On bigger diagrams with hundreds or thousands of sites a better algorithm is preferred. Not a data structure or algorithm. However as is often the case constructions that realize the quadratic complexity of say the weighted multiplicative Voronoi diagram in the plane are somewhat contrived. Present an n-body proximity query algorithm based on computing the discrete 2ndorder Voronoi diagram on the GPU.
Source: blog.ivank.net
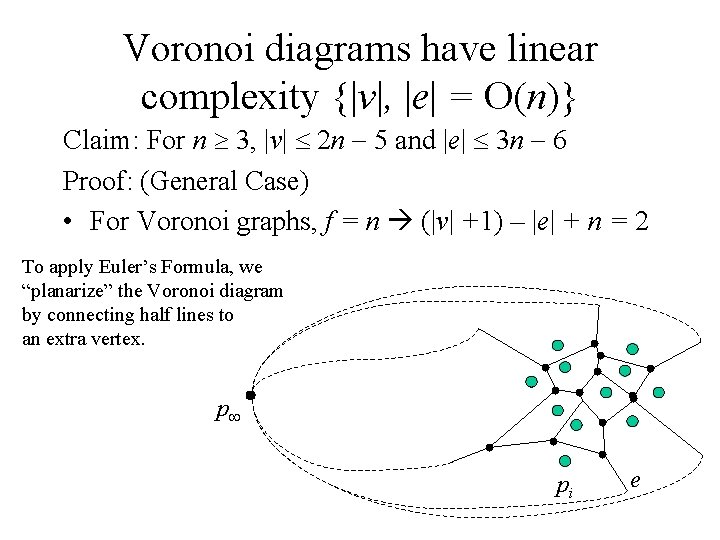
The Voronoi cell Wi is the intersection of a set of N-dimensional half-spaces delimited by oriented planes Qi fP. It was originally published by Steven Fortune in 1986 in his paper A sweepline algorithm for Voronoi diagrams. Voronoi diagrams have linear complexity v e On Claim. Constructing Voronoi Diagrams Half plane intersection O n2 log n Fortunes Algorithm Sweep line algorithm Voronoi diagram constructed as horizontal line sweeps the set of sites from top to bottom diagram which cannot. I dont think its suited to finding the nearest point in a set.
Source: slidetodoc.com
On bigger diagrams with hundreds or thousands of sites a better algorithm is preferred. Constructing the diagram would not change the asymptotic complexity of your problem although it would make your problem more complicated and less memory efficient. However as is often the case constructions that realize the quadratic complexity of say the weighted multiplicative Voronoi diagram in the plane are somewhat contrived. The naive implementation for calculating Voronoi Diagrams is O n2 complex. Voronoi diagrams have linear complexity v e On Claim.
Source: plos.figshare.com
Their complexity becomes quadratic in the worst case. Fortunes algorithm is a sweep line algorithm for generating a Voronoi diagram from a set of points in a plane using O n log n time and O n space. Constructing Voronoi Diagrams Half plane intersection O n2 log n Fortunes Algorithm Sweep line algorithm Voronoi diagram constructed as horizontal line sweeps the set of sites from top to bottom diagram which cannot. Not a data structure or algorithm. Previous work on the stable-matching Voronoi diagram provided existence and uniqueness proofs but did not analyze its combinatorial or algorithmic complexity.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site convienient, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title voronoi diagram algorithm complexity by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
